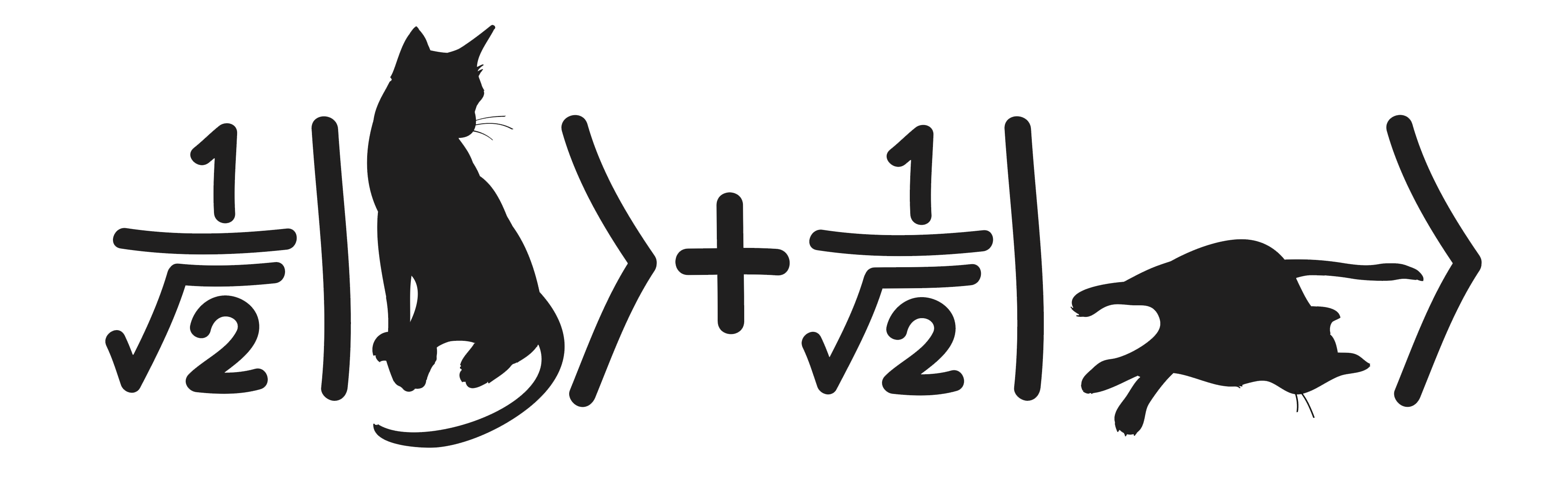
Table of contents
Lecture notes ^
There is no required textbook for this course. The official course lecture notes, written by the lecturer, will contain everything you need to know. References to textbooks for additional study beyond the course material may be given as needed.
Update 2022: After teaching this course, I continued to update and expand these notes. The new and improved notes can be downloaded here.
Schedule and logistics ^
Lectures will be given every Monday and Wednesday from 1:00pm to 3:00pm, from May 4th to June 15th, 2020. There will be no lecture on May 18th, due to Victoria Day.
Tutorials will be given every Monday and Wednesday from 3:00pm to 4:00pm, with the same schedule as the lectures. There will be a total of 24 hours of lectures and 12 hours of tutorials. The students will split into two groups for the tutorials.
The course will be taught online via Zoom, due to the ongoing COVID-19 pandemic. Students will receive information on how to attend the Zoom meetings via email, and the information will also be on Quercus. The meetings will be protected by a password to prevent Zoombombing. Please do not share the meeting ID or password with anyone who is not a student in this course.
The live lectures will be recorded and made available to watch at your leisure. Links to the recordings will be posted below. However, it is highly recommended to attend the live lectures if possible, so that you can ask questions and interact with the lecturer.
The recordings will be posted publicly on YouTube. However, any interaction with students will be edited out unless you explicitly ask to be included in the recording. Therefore, please feel free to ask as many questions as you want during the lectures; your questions will not be made public.
Please click here for the course listing on the University of Toronto website.
Lecturer and teaching assistants ^
The lecturer for this course is Barak Shoshany. I received my PhD in theoretical physics from Perimeter Institute in Waterloo, where I also work as a postdoctoral researcher. I had research internships at Tel Aviv University and Weizmann Institute of Science in Israel and CERN in Switzerland. My research interests currently include general relativity, quantum gravity, and scientific computing.
My office hours are every Tuesday from 11:00am to 1:00pm. These will be virtual office hours, held via Zoom using the same meeting ID and password as the lectures. Please feel free to come to the office hours with any questions or concerns.
Outside of the office hours, you are always welcome to email me at barak.shoshany@utoronto.ca. I will do my best to reply to all student emails as soon as possible. In addition, if you wish to schedule a 1-on-1 video chat, please do not hesitate to email me.
The teaching assistants are Aaron Goldberg and Jyotirmoy Roy. Both of them would be happy to answer any questions you may have by email. They will also hold virtual office hours before the mid-term and the final assessment. If needed, you may ask the teaching assistants to schedule 1-on-1 video chats by emailing them.
Course outline ^
This course will serve as a comprehensive introduction to the foundations of quantum mechanics, from the modern point of view of 21st century theoretical physics. It will be somewhat different from a traditional first course in quantum mechanics, in that we will develop the theory from scratch in an axiomatic and mathematically rigorous(ish) way. There will be less emphasis on doing calculations, and more on a deep conceptual understanding of the theory.
First, a short non-technical overview of quantum mechanics will be provided. We will discuss the failures of classical mechanics that prompted the development of the quantum theory, and list the major differences between classical and quantum mechanics.
Next, we will learn the necessary mathematical background, including complex numbers, linear algebra, and probability. Even if you took courses on these subjects before, you should still pay careful attention, since we will learn the material from the quantum point of view and introduce important notation that is unique to quantum mechanics.
Once we have a firm grasp of the mathematical background, we will use it to define quantum mechanics axiomatically. We will learn about fundamental concepts such as Hilbert spaces, states, operators, observables, superposition, probability amplitudes, and expectation values.
Then, we will begin studying simple discrete quantum systems known as qubits, which are the quantum analogue of bits, and are used in quantum computers. We will learn about Schrödinger's cat, quantum entanglement, Bell's theorem, the uncertainty principle, unitary evolution, quantum measurements, and quantum teleportation.
In the remainder of the course we will study simple continuous quantum systems and related phenomena, including Hamiltonians, the Schrödinger equation, the quantum harmonic oscillator, wavefunctions, the wave-particle duality, quantum interference, and scattering and tunneling in one dimension.
If time permits, we will touch on exciting advanced topics such as canonical quantization, path integrals, quantum algorithms, particle physics, quantum field theory, and/or quantum gravity.
By the end of the course, the students should expect to have a fairly good understanding of quantum mechanics, and to develop an intuition for this very strange and unintuitive theory. They will also be adequately prepared to dive deeper into the subject, whether by taking more advanced courses or by doing research.
Grading ^
There will be 6 weekly homework assignment, consisting of a subset of the problems provided in the lecture notes. Submitted solutions will be marked as "pass" or "fail" only. The homework assignments have a strict deadline, and late submissions will not be accepted. I will post the correct solutions shortly after the deadline.
You are strongly encouraged to solve all of the homework assignments in order to make sure you understand the material. Collaboration with other classmates is allowed, as long as it is clearly specified exactly which students worked together and how much each of them contributed. Please note that questions from the homework may appear in the assessments.
There will be a midterm and a final assessment, both in the form of oral assessments via 1-on-1 Zoom meetings with the lecturer. The oral assessments will be recorded for grading purposes, but will not be posted anywhere. Dates for the mid-term and the final will be posted later; the final will take place some time between June 17th and June 25th.
The midterm will be 10 minutes long, and the final will be 15 minutes long. During both, I will simply ask you a few questions to see if you understand the material. One of the goals of the midterm will be to introduce you to the oral assessment format and prepare you for the final assessment.
As some of the students currently live in different time zones, attendance to the live online lectures or tutorials will not affect to the final grade. The final grade will consist of:
- 18%: homework assignments (3% for each "pass"),
- 22%: midterm oral assessment,
- 60%: final oral assessment.
Homework assignments ^
The homework assignments will be given as selected exercises and problems from the course lecture notes. However, you are strongly encouraged to solve all of the exercises and problems in the notes, even those that were not given as homework! Also, it is highly recommended to typeset your homework solutions using LyX.
Homework solutions should be submitted through Quercus.
Homework 1 (due by Saturday, May 23rd, noon Eastern Time): Exercise/Problem no. 3.2, 3.20, 3.21, 3.23, 3.26, 3.27, 3.29, 3.30, 3.31, 3.32, 3.34, 3.39.
Homework 2 (due by Saturday, May 30th, noon Eastern Time): Exercise/Problem no. 3.41, 3.44, 3.45, 3.46, 3.47, 3.52, 3.55, 3.56, 3.61, 3.62, 3.63, 3.64. Problem 3.65 is optional, but if solved correctly will give an automatic "pass" on this assignment.
Homework 3 (due by Saturday, June 6th, noon Eastern Time): Exercise/Problem no. 4.4, 4.6, 4.10, 4.12, 4.13, 4.16, 4.20, 4.21, 4.22, 4.23, 4.24, 4.25.
Homework 4 (due by Saturday, June 13th, noon Eastern Time): Exercise/Problem no. 4.28, 4.33, 4.34, 4.35, 4.37, 4.42, 4.46, 4.47, 4.50, 4.51, 4.52, 4.53. Problem 4.54 is optional, but if solved correctly will give an automatic "pass" on this assignment.
Homework 5 + Final Project (due by Thursday, June 25th, noon Eastern Time): Exercise/Problem no. 5.8, 5.9, 5.12, 5.13, 5.15, 5.16, 5.20, 5.21, 5.22, 5.23, 5.25, 5.26, 5.27, 5.28.
Videos and materials from the lectures ^
Lecture 1/12: A Non-Technical Overview of Quantum Physics; Quantum vs. Classical Mechanics (Monday, May 4th, 2020)
In this lecture I provide a non-technical overview of quantum physics. First, I discuss four experimental results which demonstrated that classical physics fails to describe reality: black-body radiation, the photoelectric effect, the double-slit experiment, and the Stern-Gerlach experiment. Then, I provide a detailed comparison of the properties of quantum vs. classical mechanics. The material corresponds to chapter 2 of the lecture notes.
Lecture 2/12: Mathematical Background for Quantum Theory, Part 1 (Wednesday, May 6th, 2020)
In this lecture I cover some of the mathematical background required to understand quantum theory, including complex numbers, complex vectors, the inner product, Hilbert spaces, orthonormal bases, complex matrices, the adjoint, the outer product, the completeness relation, representing vectors in different bases, change of basis, and multiplication and inverse of matrices. The material corresponds to sections 3.1 and 3.2.1-3.2.9 of the lecture notes.
Lecture 3/12: Mathematical Background for Quantum Theory, Part 2 (Monday, May 11th, 2020)
In this lecture I cover the rest of the mathematical background required to understand quantum theory. From linear algebra, I discuss matrices inside inner products, eigenvalues and eigenvectors, Hermitian, unitary, and normal matrices, representing matrices in different bases, diagonalizable matrices, and the Cauchy-Schwarz inequality. From probability theory, I talk about random variables, probability distributions, conditional probability, and expected values. The material corresponds to sections 3.2.10-3.2.17 and 3.3.1-3.3.3 of the lecture notes.
Lecture 4/12: Quantum Systems, States, Operators, Observables, and Probability (Wednesday, May 13th, 2020)
In this lecture, I first cover the final two topics of the required mathematical background: standard deviation and normal distributions. Then the real fun begins! After a brief explanation about dimensionless and dimensionful constants, I start defining quantum theory axiomatically. First, I define quantum systems, quantum states, and quantum operators. Then, I explain how Hermitian operators are related to physical observables, and how to calculate the probabilities for different measurement outcomes of these observables. The material corresponds to sections 3.3.4-3.3.5 and 4.1.1-4.1.4 of the lecture notes.
Lecture 5/12: Probability Amplitudes, Quantum Superposition, Spin, and Qubits (Wednesday, May 20th, 2020)
In this lecture I discuss the meaning of probability amplitudes, the concept of superposition of quantum states, and how to calculate expectation values for observables. Then, I introduce two-state systems, the Pauli matrices, spin, and qubits - the quantum analogues of bits, which are used in quantum computing. I finish by discussing the conceptual meaning of superposition. The material corresponds to sections 4.1.5-4.1.7 and 4.2 of the lecture notes.
Lecture 6/12: Tensor Products, Quantum Entanglement, Bell States, and a Common Misconception (Monday, May 25th, 2020)
In this lecture I discuss composite systems, the tensor product, quantum entanglement, separable vs. entangled states, the Bell states, and the common misconception that quantum entanglement allows faster-than-light communication. The material corresponds to sections 4.3.1-4.3.5 of the lecture notes.
Lecture 7/12: Bell's Theorem, Hidden Variable Theories, and the Uncertainty Principle (Wednesday, May 27th, 2020)
In this lecture I prove Bell's theorem, which shows that quantum entanglement is stronger than classical correlation and rules out local hidden variable theories, and the uncertainty principle. The material corresponds to sections 4.3.6 and 4.4.1-4.4.2 of the lecture notes.
Lecture 8/12: Dynamics, Unitary Evolution, and Quantum Logic Gates (Monday, June 1st, 2020)
In this lecture I begin the discussion of dynamics in quantum theory by introducing unitary transformations and evolution, with examples in the form of one-qubit and two-qubit quantum logic gates. The material corresponds to sections 4.5.1-4.5.2 of the lecture notes.
Lecture 9/12: Measurements, Interpretations of Quantum Mechanics, and the No-Cloning Theorem (Wednesday, June 3rd, 2020)
In this lecture I discuss projective measurements, collapse, the measurement problem, interpretations of quantum mechanics, Schrödinger’s cat, and the no-cloning theorem. The material corresponds to sections 4.5.3-4.5.7 and 4.6.1 of the lecture notes.
Lecture 10/12: Quantum Teleportation, Exponentials and Logarithms of Matrices and Operators (Monday, June 8th, 2020)
In this lecture I discuss quantum teleportation, summarize what we have learned so far regarding discrete systems, and then begin the introduction of continuous quantum systems by defining exponentials and logarithms of complex numbers, matrices, and operators. The material corresponds to sections 4.6.2, 4.7, and 5.1 of the lecture notes.
Lecture 11/12: Hamiltonians, the Schrödinger Equation, and Canonical Quantization (Wednesday, June 10th, 2020)
In this lecture I define the Hamiltonian in terms of the unitary evolution operator, and use that relation to derive the Schrödinger equation from scratch. I also discuss time-independent Hamiltonians, time-related symmetries, and energy eigenstates. Then, I review classical Hamiltonian mechanics and motivate canonical quantization. Finally, I discuss the classical harmonic oscillator in preparation for its quantization in the next lecture. The material corresponds to sections 5.2, 5.3, and 5.4.1 of the lecture notes.
Lecture 12/12: The Harmonic Oscillator, Wavefunctions, and Solving the Schrödinger Equation (Monday, June 15th, 2020)
In this lecture I present the quantum harmonic oscillator, its energy eigenstates, and the ladder or creation/annihilation operators. I explain how to generalize what we have learned from discrete to continuous systems. Then, I talk about the position and momentum operators, and the relation between wavefunctions and states. I also explain quantum interference and how it relates to the double-slit experiment. Finally, I discuss solutions to the Schrödinger equation. The material corresponds to sections 5.4.2-5.4.3, 5.5, and 5.6 of the lecture notes.
Practice Session for the Final Assessment (Tuesday, June 16th, 2020)
The questions I asked during the practice session, along with the answers, can be found here (PDF format).